据报道，一个由美英两国三名计算机专家组成的研究团队最近宣称他们证明了“毕氏三元数问题(Pythagorean triples problem)”。他们分别是德克萨斯大学的玛里金·休尔、肯塔基大学的维克多·马雷克和斯旺西大学的奥利弗·库尔曼，其成果发表在全球最大的预印本网站arXiv上，并在法国波尔多召开的一次会议上演示了证明结果。

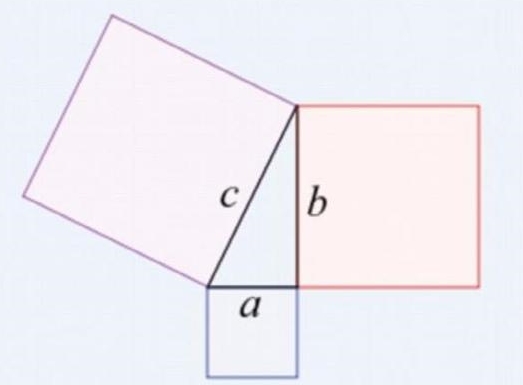
毕氏三元数问题是毕达哥拉斯定理(也称“勾股定理”)方面的著名问题，即关于直角三角形各条边的长度之间的关系问题。在平面直角三角形中，两个直角边边长的平方加起来等于斜边长的平方，即著名的数学表达式：a^2+b^2=c^2。这一问题在1917年由德国数学家伊赛·舒尔提出，问的是：能否将所有正整数分成两个部分，其中所有毕氏三元数组(即满足a^2+b^2=c^2的a,b,c三个数)都不处于同一部分？否则，最小的反例是什么？

上世纪80年代，美国数学家罗纳德·格雷厄姆也提出一个疑问：如果每一条边长都是一个正整数，并给这个正整数分配一种颜色，或蓝色或红色，满足上述表达式的正整数是否都是同一颜色呢？不过，他认为答案是否定的。简单地说，满足上述公式的任何三个正整数，只可能是两个是一种颜色，另一个是另外一种颜色，它们不可能是相同颜色的。格雷厄姆还悬赏100美元，请数学爱好者帮助他解决一个数学疑问，因为它已困扰了格雷厄姆很长时间。30多年来，一直未能有人拿出解答方案前来领赏。

毕氏三元数问题常被转化为着色问题。例如，3的平方加4的平方等于5的平方;如3和4是红色，5就得是蓝色，不能三个数字全是蓝色或红色。研究者发现，从1到7824的所有正整数都能被用这种方式归类。在这7824个方格中，没有任何满足a^2+b^2=c^2的三个数同为蓝色或同为红色(白色数字不属于毕氏三元数)。遗憾的是，他们未能解答为什么当数字超过7824时，会出现无解的现象。

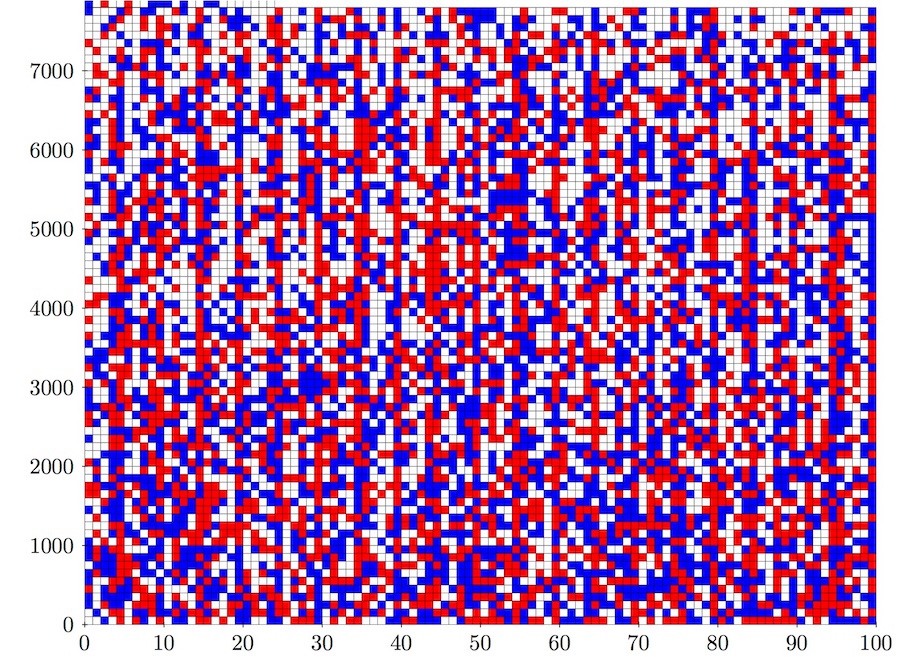
图：毕氏三元数问题被转化为着色问题

休尔等三名计算机专家是借助超级计算机来证明毕氏三元数问题的。据悉，证明文件的字符总和相当于美国国会图书馆所有数码资料的总和，大小约200TB，这也是人类迄今得到的最“长”的一个“数学证明”。即使利用德州先进运算中心的Stampede超级计算机对这些数据进行压缩，也需要花两天时间。如果阅读全部的证明文件，就得花10亿年的功夫。

由上可见，计算机的应用，既改变了数学研究的方法，也提高了数学研究的效率。众所周知，数学是计算机科学的理论基础,回顾计算机发展史,其中的每一次飞跃都离不开数学的贡献。有趣的是，计算机的出现反过来给予人们另外一种探索数学规律的手段。

计算机的发明，是为计算而来，而计算能力始终是计算机的根本。计算机的介入，扩展了数学研究的领域，促进了计算数学的发展。尤其是运算量极其庞大的数学问题，大多数情况只能借助计算机来解决。例如，四色问题、E8结构、费克特(Fekete)问题、开普勒(Kepler)猜想、埃尔德什差异(discrepancy)问题等著名数学难题，都是借助计算机来破解的。值得一提的是，当今的大素数只能借助计算机尤其互联网来探究。例如，美国中央密苏里大学数学家柯蒂斯·库珀最近就借助网格计算技术发现了目前已知的最大素数2^74207281－1，该数有22338618位。

计算机成为数学研究的工具已是大势所趋，不可阻挡。正如中国科学家及未来学家周海中在《21世纪数学展望》一文中所言：计算机在数学研究中发挥的作用将越来越大;借助计算机解决数学问题将激励人们去寻求更好、更简单的方法，也加深人们对数学本质特征的认识，还推动以计算机为基础的人工智能的发展。毫无疑问，在计算机的助力下，破解数学难题的成果今后会越来越多。

最后一提的是，也许有人会问：借助计算机破解数学难题，这样“正确”的证明，还算不算是“数学”？由于数据的绝对量过于庞大，以至于没有办法由人工进行验证，那么这种证明能否被验证真伪？如果数学家的工作是通过理论帮助人类更好地理解数学，那通过穷举来解决问题的计算机究竟有什么存在的意义？或许我们只能希望早日有人能给出数学问题的逻辑推理。例如，2014年英国计算机专家阿列克谢·利什特沙和鲍里斯·科涅夫借助超级计算机证明了埃尔德什差异问题;一年后，美国加州大学洛杉矶分校数学家陶哲轩就用传统方式成功破解了这一难题，此事震动了全球数学界。

文章链接：

Marijn J. H. Heule, et al, "Solving and Verifying the boolean Pythagorean Triples problem via Cube-and-Conquer," SAT 2016, LNCS 9710, pages 228-245, DOI: 10.1007/978-3-319-40970-2_15

（本文来源：人民网；）

如若转载，请注明e科网。

如果你有好文章想发表or科研成果想展示推广，可以联系我们或免费注册拥有自己的主页