科幻图片:利用石墨烯滑雪板在石墨烯高速公路上无摩擦滑动,实现星际漫游。意在展现石墨烯超滑技术可能具有潜在的应用前景。
清华新闻网2月16日电 近日,清华大学机械工程系、摩擦学国家重点实验室联合中国科学院化学研究所等单位,在利用石墨烯实现固体超滑领域取得重要进展。相关研究成果以“利用镀有石墨烯的微球在高接触压力下实现鲁棒性的微观超滑”为题于2月14日发表在《自然·通讯》。
该研究中,研究人员设计并制备出一款用于原子力显微镜的镀有石墨烯的微球探针,实现了石墨烯与石墨烯之间微观摩擦力的测量,并且获得了拥有“鲁棒”特性的超低摩擦:适用于较宽范围的载荷、环境气氛、湿度、扫描范围以及速度等实验条件,同时超滑状态也可以维持较长时间。此外这种石墨烯探针也可以在其他二维材料,如六方氮化硼(h-BN)晶体上获得超滑,从而实现了异质二维材料之间的摩擦测量。
据统计,全球约1/3的一次性能源由摩擦消耗,愈演愈烈的能源危机更突显了摩擦学研究的现实意义。超滑是揭示摩擦能量耗散的起源以及探索降低摩擦能耗途径的重要研究方向。近年来二维材料因其层间弱范德华作用以及优异的摩擦学特性引起了广泛关注。如何实现稳定持久、对环境气氛不敏感的超滑状态,对实现石墨烯超滑的应用有着重要意义。
清华大学摩擦学国家重点实验室联合中科院化学所设计并制备出了镀有石墨烯的原子力显微镜微球探针。利用无金属催化的方法直接在氧化硅微球上生长多层多晶石墨烯,再将石墨烯微球粘在无探针的悬臂梁上。此种制备方法避免了石墨烯转移过程引入的杂质,同时石墨烯与基底具有较好的膜基结合力。
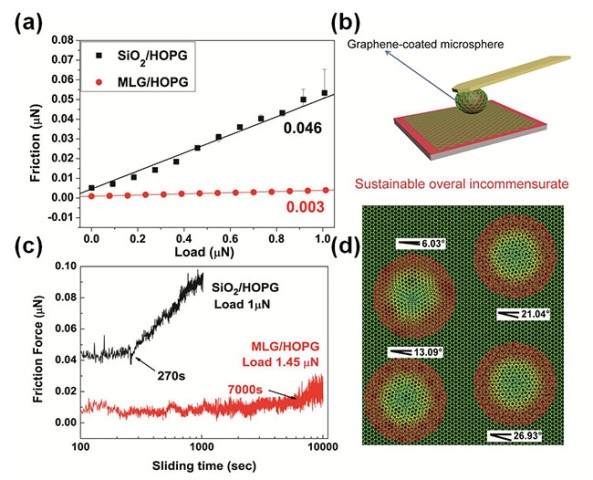
图:实验和模拟结果(a)摩擦力随着载荷变化曲线;(b)石墨烯探针示意图;(c)摩擦力随时间的变化曲线;(d)分子动力学模拟多粗糙峰多晶接触模型(每个粗糙峰上包覆的石墨烯晶格取向随机分布)。
石墨烯微球探针在对天然石墨、高定向热解石墨(HOPG)、机械剥离石墨烯以及六方氮化硼晶体的摩擦实验中均获得了超低摩擦(摩擦系数最低可达0.003)。这种超低摩擦不受探针与基底之间的相对转角的影响,同时超滑状态能够在较高粗糙峰接触压力下持续较长时间。通过高分辨AFM原子取向分析、接触力学计算和分子动力学模拟,研究人员揭示了这种持久稳定的超低摩擦机理:石墨烯微球表面的多粗糙峰形貌以及石墨烯的多晶结构使得石墨烯微球与样品间形成一种稳定的“准非公度接触”,即多粗糙峰包覆石墨烯随机取向的接触状态。另外,超滑的实验结果不易受环境气氛和湿度影响,能够在干燥氮气、大气和潮湿空气(相对湿度51%)下实现,这种现象或可归因于石墨烯探针与石墨基底的双面疏水特性。该研究为固体润滑和超滑系统设计提供了新的思路,此外该石墨烯探针方法同样可推广到其他二维材料或者异质二维材料间的固体超滑研究。
清华大学机械系副教授马天宝、中国科学院化学研究所研究员于贵、以及清华大学机械系教授雒建斌为该论文的通讯作者。该论文的第一作者为清华大学机械系博士生刘淑娓,第二作者为中国科学院化学研究所博士生王华平。此论文是继2016年10月在《自然·通讯》发表“莫尔条纹稳定石墨烯超低摩擦状态”论文后,该课题组在二维材料固体超滑领域的又一重要进展。该工作得到国家自然科学基金委重大科研仪器研制项目、基金委重大项目、973项目、基金委优秀青年基金、万人计划青年拔尖人才项目、摩擦学国家重点实验室自主研究课题等相关研究计划支持。分子动力学模拟在清华大学高性能计算中心“探索100”平台上完成。
文章链接:
Shu-Wei Liu, et al, "Robust microscale superlubricity under high contact pressure enabled by graphene-coated microsphere," Nature Communications 8, Article number: 14029 (2017), doi:10.1038/ncomms14029
(本文来源:清华大学新闻网;)
如若转载,请注明e科网。
如果你有好文章想发表or科研成果想展示推广,可以联系我们或免费注册拥有自己的主页
- 清华大学
- 石墨烯


 我要投稿
我要投稿